Euler's method

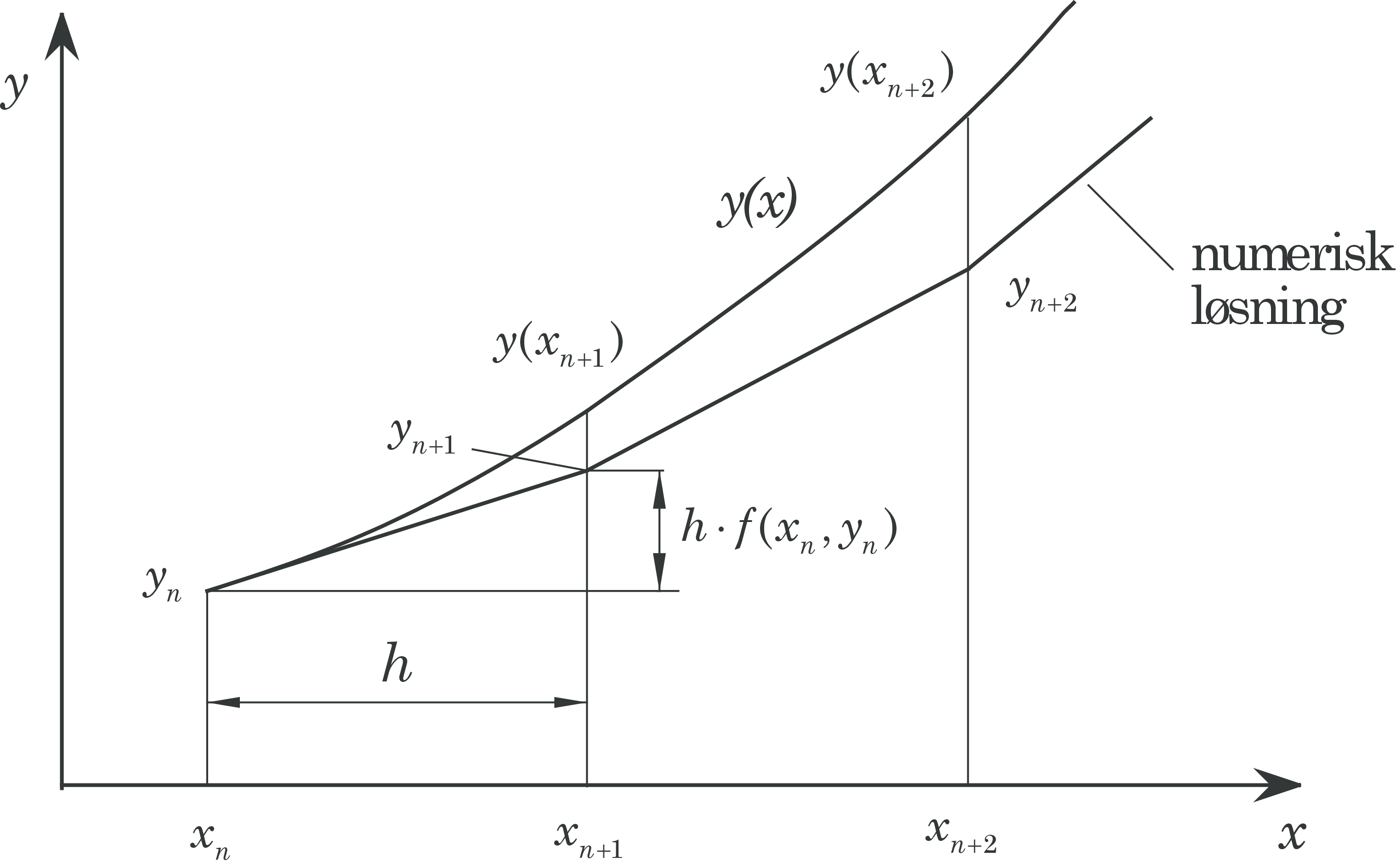
The ODE is given as $$ \begin{align} \tag{40} \frac{dy}{dx} = y'(x)&=f(x,y)\\ y(x_0)=&y_0 \end{align} $$ By using a first order forward approximation (19) of the derivative in (40) we obtain: $$ \begin{equation*} y(x_{n+1})=y(x_n)+h\cdot f(x_n,y(x_n))+O(h^2) \end{equation*} $$ or $$ \begin{equation} \tag{41} y_{n+1}=y_n+h\cdot f(x_n,y_n) \end{equation} $$ (41) is a difference equation and the scheme is called Euler's method (1768). The scheme is illustrated graphically in Figure 3. Euler's method is a first order method, since the expression for $ y'(x) $ is first order of $ h $. The method has a global error of order $ h $, and a local of order $ h^2 $.

Figure 3: Graphical illustration of Euler's method.