Numerical Methods for Engineers

 

 

 

Runge-Kutta of 4th order

Euler's method and Heun's method belong to the Runge-Kutta family of explicit methods, and is respectively Runge-Kutta of 1st and 2nd order, the latter with one time use of corrector. Explicit Runge-Kutta schemes are single step schemes that try to copy the Taylor series expansion of the differential equation to a given order.

The classical Runge-Kutta scheme of 4th order (RK4) is given by $$ \begin{align} &k_1=f(x_n,y_n)\nonumber\\ &k_2=f(x_n+\frac{h}{2}, y_n+\frac{h}{2}k_1)\nonumber\\ \tag{62} &k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2)\\ &k_4=f(x_n+h,y_n+hk_3)\nonumber\\ &y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\nonumber \end{align} $$

We see that we are actually using Euler's method four times and find a weighted gradient. The local error is of order \( O(h^5) \), while the global is of \( O(h^4) \). We refer to [5].

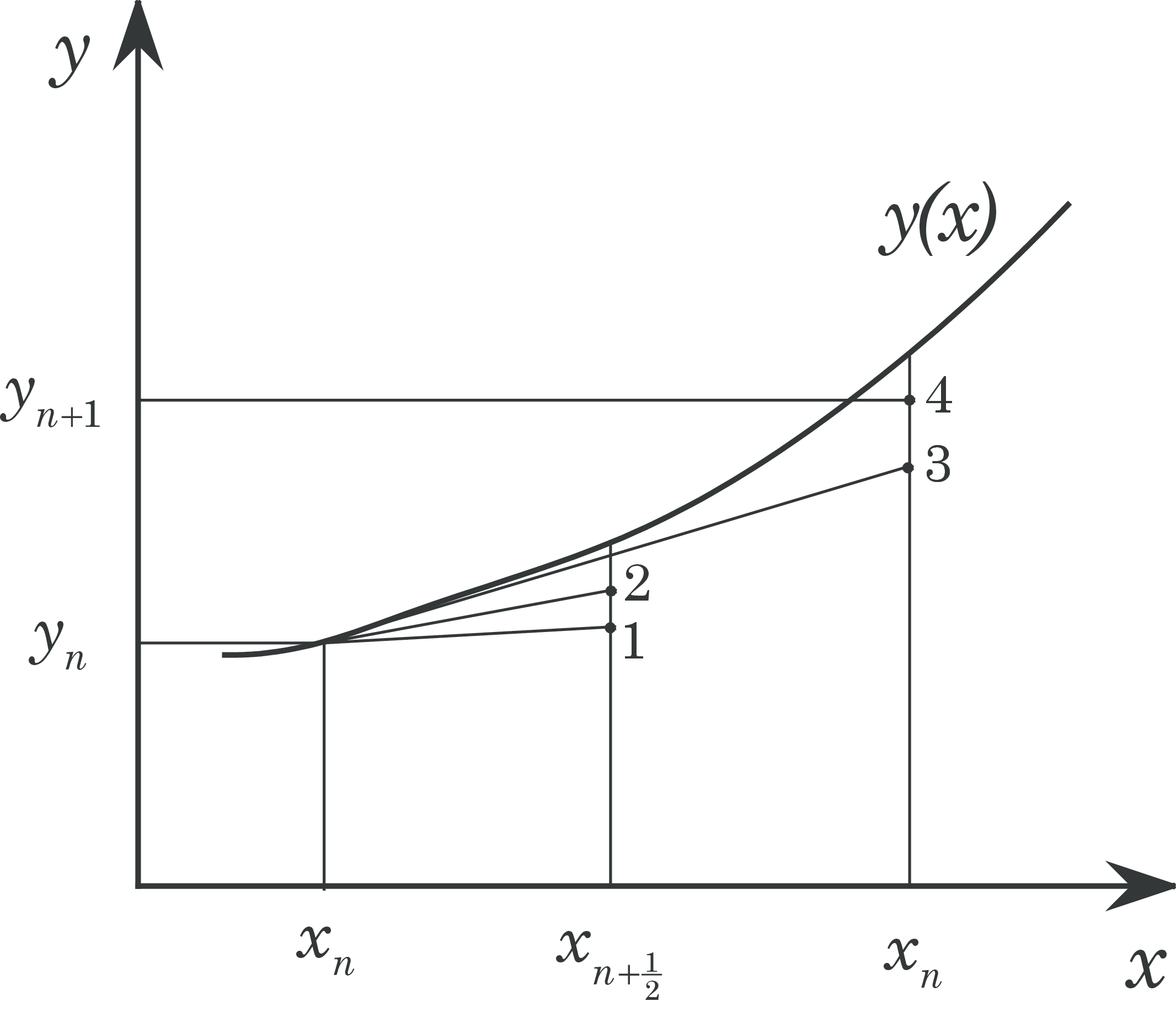
Figure 9 shows a graphical illustration of the RK4 scheme.

In detail we have

  1. In point \( (x_n,y_n) \) we know the gradient \( k_1 \) and use this when we go forward a step \( h/2 \) where the gradient \( k_2 \) is calculated.
  2. With this gradient we start again in point \( (x_n,y_n) \), go forward a step \( h/2 \) and find a new gradient \( k_3 \).
  3. With this gradient we start again in point \( (x_n,y_n) \), but go forward a complete step \( h \) and find a new gradient \( k_4 \).
  4. The four gradients are averaged with weights \( 1/6 \), \( 2/6 \), \( 2/6 \) and \( 1/6 \). Using the averaged gradient we calculate the final value \( y_{n+1} \).
Each of the steps above are Euler steps.

Figure 9: Illustration of the RK4 scheme.

Using (62) on the equation system in (52) we get $$ \begin{align} &(y_1)_{n+1}=(y_1)_n +\frac{h}{6}(k_1+2k_2+2k_3+k_4) \nonumber\\ &(y_2)_{n+1}=(y_2)_n +\frac{h}{6}(l_1+2l_2+2l_3+l_4) \tag{63} \\ &(y_3)_{n+1}=(y_3)_n +\frac{h}{6}(m_1+2m_2+2m_3+m_4) \nonumber\\ \end{align} $$ where $$ \begin{align*} k_1&=y_2 \\ l_1&=y_3 \\ m_1&=-y_1y_3\\ \\ k_2&=(y_2+hl_l/2)\\ l_2&=(y_3+hm_1/2)\\ m_2&=-[(y_1+hk_1/2)(y_3+hm_1/2)]\\ \\ k_3&=(y_2+hl_2/2)\\ l_3&=(y_3+hm_2/2)\\ m_3&=-[(y_1+hk_2/2)(y_3+hm_2/2)]\\ \\ k_4&=(y_2+hl_3)\\ l_4&=(y_3+hm_3)\\ m_4&=-[(y_1+hk_3)(y_3+hm_3) \end{align*} $$